Простой пример оптимального решения

Допустим, мы имеем о сигнале следующую информацию: сигнал может иметь только два уровня напряжения 0 или 1 с равной вероятностью, смена уровней происходит мгновенно и в случайные моменты времени, при проходе по линии связи сигнал складывается с белым шумом с известным законом плотности распределения вероятностей. Задача - периодически измерять значение приходящего сигнала искаженного шумом и делать оценку его истинного значения при минимуме ошибок.

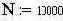
	-количество выборок
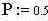
	-вероятность появления сигнала с уровнем 1
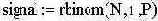
	-используем биноминальное распределение для моделирования сигнала
Гистограмма сигнала. h – массив данных для построения гистограммы (см. исходный mcd файл)

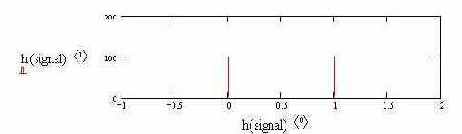
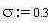
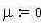
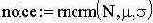
		- смоделируем шум где m - мат ожидание, s- стандартное отклонение

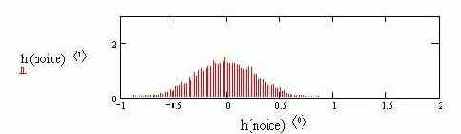Гистограмма шума

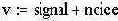- выходной сигнал равен смеси сигнала с шумом

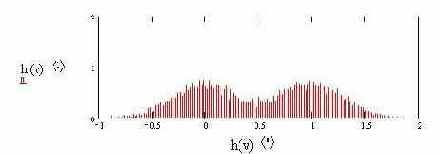Гистограмма смеси сигнал-шум

Понятно, что плотность распределения наблюдаемого сигнала подчиняется закону полной вероятности и выражается формулой

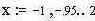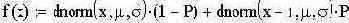- здесь:

- условные плотности вероятности наблюдаемого сигнала при условии, что истинный имеет уровень 0 и 1 соответственно.

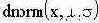
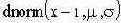
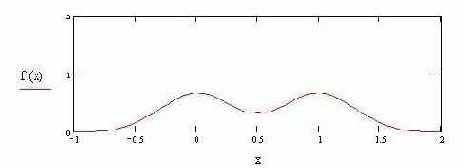
Задача наблюдателя определить некоторую границу относительно которой принимается решение об истинном значении сигнала. Граница должна быть оптимальной в смысле наименьшего количества ошибок в процессе оценки сигнала.

Допустим:

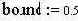		- выбранная граница. Если значение сигнала превысило границу, то считаем, что истинное значение равно 1, если нет, то считаем истинным значением 0

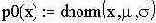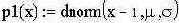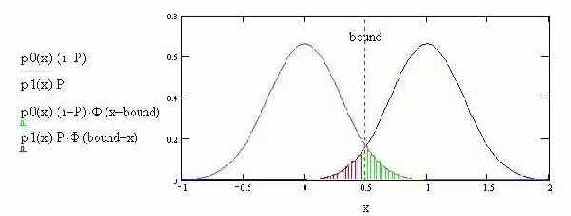При данной границе вероятность ошибки будет равна суме площадей заштрихованных красным и зеленым цветом. Площадь красной области равна вероятности суждения о том, что истинное значение сигнала равно 0, в то время как он равен 1. Площадь зеленой области равна вероятности суждения о том, что истинное значение сигнала равно 1, в то время как он равен 0.

Очевидно, что минимальная вероятность ошибки будет в том случае, если граница будет выбрана в той же точке, где пересекаются кривые двух распределений. Отношение p1(x)/p0(x)

называют отношением правдоподобия. Оно показывает насколько правдоподобнее предположение о приеме сигнала 1, чем альтернативное предположение о приеме сигнала 0.

Данный подход называют байесовым методом, упоминание о котором можно встретить в некоторых публикациях по АОНам.

Однако вся сложность алгоритма определяется не им.

Содержание раздела